Unraveling The Mystery: What Does X*x*x = 2 Really Mean?
In the vast and often captivating world of mathematics, some equations appear deceptively simple at first glance, yet hold a surprising depth once you begin to unravel them. One such intriguing enigma is the equation x*x*x is equal to 2. You might also see it written as X * x * x = 2, or more compactly, x³ = 2. This seemingly straightforward statement beckons us to discover its hidden meaning and the profound implications of its solution.
For both seasoned mathematicians and curious newcomers, this equation continues to captivate and challenge. It's a perfect example of how a few symbols can open up a discussion about fundamental mathematical concepts, from the nature of numbers to the very tools we use to solve problems. Our objective today is to determine the precise value of ‘x’ that makes this equation a true statement, where the cubed value of ‘x’ indeed equals 2, and to understand why its solution is so significant.
Understanding the Equation: x*x*x = 2
Before we dive into solving for 'x', let's break down what x*x*x = 2 actually represents. This equation involves two key components: the variable 'x' and the constant '2'.
The Basics of Cubing
The expression x*x*x is a shorthand way of saying "x multiplied by itself three times." In mathematical terms, this is known as "x cubed" or x³. It's a fundamental operation in algebra, much like squaring a number (multiplying it by itself twice, e.g., x*x or x²).
- If
x = 2, thenx*x*xwould be2 * 2 * 2, which equals8. - Similarly, if
x = 3, thenx*x*xwould be3 * 3 * 3, resulting in27.
In our equation, x isn't a known number like 2 or 3; it's a placeholder for an unknown value that, when multiplied by itself three times, gives us exactly 2.
The Constant Companion: The Number 2
On the other side of the equation, we encounter the number 2. This is a constant, meaning its value is fixed and doesn't change. It serves as a fixed point of reference within the mathematical equation. Our goal is to find an 'x' that, when cubed, perfectly matches this constant value.
The Quest to Solve for x
Now that we understand the components, the central question arises: how do we find 'x'? This is what "solving for x" means—isolating the variable to discover its precise numerical identity.
What Does "Solve for x" Mean?
To solve for x in x³ = 2 means to find the number which, when multiplied by itself three times, equals 2. It's like asking: "What number, when cubed, gives me 2?"
The Power of the Cube Root
To undo the operation of cubing, we use its inverse: the cube root. Just as addition undoes subtraction, and multiplication undoes division, the cube root undoes cubing. The symbol for the cube root is ∛.
If x³ = 2, then to find 'x', we take the cube root of both sides of the equation:
x = ∛2
This is the exact mathematical solution. But what kind of number is ∛2?
The Nature of the Solution: An Irrational Discovery
Now that we have obtained the solution x = ∛2, it’s essential to understand its implications. This is where the equation reveals its true depth.
What is ∛2?
The cube root of 2 is a fascinating number. If you try to find a whole number or a simple fraction that, when cubed, equals 2, you'll quickly realize there isn't one. For example:
1³ = 1 * 1 * 1 = 1(Too small)2³ = 2 * 2 * 2 = 8(Too large)
This tells us that 'x' must be a number between 1 and 2. When calculated, the cube root of 2 is approximately 1.25992104989.... The ellipsis (...) indicates that the decimal goes on forever without repeating a pattern. This characteristic defines an irrational number.
Why Irrational Numbers Matter
Irrational numbers are a cornerstone of advanced mathematics, representing quantities that cannot be expressed as a simple fraction (a ratio of two integers). Other famous irrational numbers include Pi (π) and the square root of 2 (√2).
Therefore, there are real solutions to the equation x³ = 2, but they cannot be expressed as exact, rational numbers. This concept often blurs the lines between what we perceive as "real" and "imaginary" numbers, though in this specific case, ∛2 is indeed a real number, albeit an irrational one.
Understanding this distinction is crucial for appreciating the full spectrum of numbers available in the mathematical landscape. It highlights that not every problem has a neat, whole-number answer, and that's perfectly okay!
The Broader Significance of x*x*x = 2
Beyond its direct solution, the equation x*x*x = 2 continues to hold significance in the contemporary mathematical landscape, fostering discussions and innovative ideas.
A Gateway to Mathematical Exploration
The realm of mathematics, with its labyrinthine complexities and intriguing enigmas, continues to captivate and challenge both novice and seasoned mathematicians alike. Among the myriad equations that populate this intellectual landscape, x*x*x = 2 looms as a particularly enigmatic riddle, beckoning us to explore the properties of numbers and operations more deeply. It's a simple entry point into understanding more complex polynomial equations and the nature of their roots.
Practical Applications (Briefly)
While x³ = 2 might seem like a purely academic exercise, cubic equations in general have wide-ranging applications. For instance:
- Volume Calculations: If you know the volume of a cube and want to find its side length, you'd use a cube root. If a cube has a volume of 2 cubic units, its side length would be
∛2. - Engineering and Physics: Cubic equations appear in models describing various physical phenomena, from fluid dynamics to material properties.
The Role of Calculators and Tools
In today's digital age, solving equations like x³ = 2 is made easier with advanced tools. Online "solve for x" calculators allow you to enter your problem and see the result instantly. These tools can handle single-variable equations or even systems of equations, providing exact answers or numerical approximations to almost any required accuracy. This accessibility helps students and professionals alike to quickly grasp solutions and explore mathematical concepts without getting bogged down in manual calculations of irrational numbers.
Conclusion
From a simple expression of multiplication, x*x*x = 2, we've embarked on a journey that reveals the beauty and complexity inherent in mathematics. We've seen that 'x' represents a specific, real number – the cube root of 2 – which is approximately 1.26. This number is not a neat integer or fraction, but rather an irrational number, extending infinitely without repetition. This characteristic is a testament to the rich and diverse nature of our number system.
The equation x³ = 2 serves as a fantastic illustration of how basic arithmetic operations can lead to profound mathematical concepts, challenging our intuition and expanding our understanding of what numbers truly are. It reminds us that mathematics is not just about finding simple answers, but about exploring the intricate relationships that govern our universe, one enigmatic riddle at a time.
Ultimately, understanding x*x*x = 2 is more than just finding a solution; it's about appreciating the elegance of mathematical principles and the endless possibilities they present for discovery and innovation.
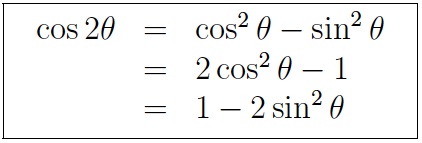
Summary of trigonometric identities
tangent to xx plus yy equals 5 at minus 2 comma 1 | Desmos

Understanding the Equal Sign - Math Coach's Corner