Unraveling The Mystery: What Does "x*x*x Is Equal To 2" Really Mean?
Mathematics often presents us with seemingly simple questions that lead to incredibly profound and fascinating answers. One such question, often encountered in algebra, is "x*x*x is equal to 2." At first glance, it might appear straightforward, but beneath its unassuming surface lies a unique mathematical entity and a journey into the heart of numerical constants. This blog post will break down this intriguing equation, explore its solution, and highlight why it's more significant than you might think.
Whether you're a student grappling with algebra, a curious mind looking to understand fundamental mathematical concepts, or just someone who enjoys a good mental puzzle, understanding "x*x*x is equal to 2" offers a glimpse into the elegance and complexity of numbers.
Deconstructing the Equation: What is `x*x*x`?
Before we dive into solving, let's clarify what "x*x*x" actually means. In mathematical notation, when a variable (like 'x') is multiplied by itself multiple times, we use exponents to simplify the expression. So:
- `x` multiplied by itself once is simply `x`.
- `x` multiplied by itself twice (`x*x`) is known as "x squared" or `x^2`. This is commonly seen when calculating the area of a square with side 'x'.
- Following this pattern, `x*x*x` is known as "x cubed" or `x^3`. This term often arises when calculating the volume of a cube with side 'x'.
Therefore, the equation "x*x*x is equal to 2" can be more concisely written as `x^3 = 2`. Our goal is to "solve for x"—that is, to find the number which, when multiplied by itself three times, equals 2.
The Quest for 'x': A Step-by-Step Solution
Solving for 'x' in `x^3 = 2` requires a specific mathematical operation that is the inverse of cubing a number. Just as subtraction is the inverse of addition, and division is the inverse of multiplication, the inverse of cubing is taking the cube root.
Isolating the Variable
Our equation is `x^3 = 2`. To find the value of 'x', we need to isolate it on one side of the equation. Currently, 'x' is "cubed." To undo this operation, we apply the cube root to both sides of the equation. This maintains the equality.
Think of it like this: if you have a number, and you cube it, and then you take its cube root, you get back to the original number. For example, the cube of 3 is 27 (`3^3 = 27`), and the cube root of 27 is 3 (`∛27 = 3`).
Introducing the Cube Root
Applying the cube root symbol (∛) to both sides of our equation:
∛(x^3) = ∛2
On the left side, the cube root cancels out the cubing operation, leaving us with just 'x':
x = ∛2
And there you have it! The answer to the equation `x*x*x is equal to 2` is `∛2`.
Verifying Your Solution
A crucial step in solving any equation is verifying your solution. To do this, substitute the value you found for 'x' back into the original equation. If both sides of the equation remain equal, your solution is correct.
Original equation: `x*x*x = 2`
Substitute `x = ∛2`:
(∛2) * (∛2) * (∛2) = 2
When you multiply the cube root of a number by itself three times, you get the original number:
2 = 2
The equation holds true, confirming that `x = ∛2` is indeed the correct solution.
The Nature of the Solution: The Enigmatic `∛2`
The number `∛2` is far more interesting than a simple integer. It is an irrational number. What does this mean?
An irrational number is a real number that cannot be expressed as a simple fraction (a ratio of two integers). When written as a decimal, it goes on forever without repeating any pattern. Famous examples include Pi (π) and the square root of 2 (√2).
While we can approximate `∛2` (it's roughly 1.259921...), it's impossible to write its exact value as a terminating or repeating decimal. This numerical constant is a unique and intriguing mathematical entity that holds the key to our equation.
The existence of such numbers highlights the complex and multifaceted nature of mathematics. While `∛2` itself is a real number, the process of finding roots for different equations can sometimes "blur the lines" between real and imaginary (or complex) numbers, inviting mathematicians to explore uncharted territories where solutions might involve components beyond the number line we typically visualize.
Beyond the Basics: Tools and Concepts for Solving Equations
While solving `x^3 = 2` by hand is straightforward, for more complex equations, various tools and concepts come into play:
- Algebra Calculators: Online "solve for x" calculators or "simplification calculators" allow you to input complex expressions and equations. They can quickly provide results, simplifying the expression to its simplest form. These tools are invaluable for checking your work or tackling problems that are too cumbersome to solve manually.
- Understanding Operations: Knowing how to isolate variables is fundamental. This involves applying inverse operations (e.g., adding to undo subtraction, dividing to undo multiplication, taking roots to undo exponents) to both sides of an equation.
- Mathematical Platforms: Many online platforms serve as unique spaces where students can interact with teachers, experts, and other students to get solutions to their queries. Whether you're preparing for board exams (CBSE, ICSE, State Boards), competitive exams (JEE, NEET), or simply struggling with a homework problem, these resources provide quick answers and detailed explanations.
The core principle remains the same: understanding the underlying mathematical logic. Calculators are great aids, but true comprehension comes from knowing *why* and *how* to apply the steps.
Why Does This Matter? The Broader Significance
You might wonder, "Why is understanding 'x*x*x is equal to 2' important?" Its significance extends beyond just finding a specific number:
- Fundamental Algebraic Concept: It introduces the concept of cubic equations and their solutions, which are foundational in higher mathematics and various scientific fields.
- Introduction to Irrational Numbers: It's an excellent example of how simple integer problems can lead to irrational solutions, expanding our understanding of the number system beyond integers and fractions.
- Problem-Solving Skills: The process of isolating 'x' and applying the correct inverse operation reinforces critical problem-solving skills applicable to many areas of life.
- Appreciation for Mathematical Depth: It demonstrates that even seemingly simple equations can hide profound mathematical truths and connections, inviting further exploration into the vast and intricate world of numbers.
Every mathematical problem, no matter how small, contributes to a larger tapestry of knowledge, pushing the boundaries of what we understand about the universe through the language of numbers.
Conclusion
The equation "x*x*x is equal to 2," or `x^3 = 2`, is a perfect illustration of how a concise mathematical statement can encapsulate a rich and intriguing answer. We've seen that its solution is the cube root of 2 (`∛2`), an irrational number that holds a special place in the real number system. The journey to find this solution involves understanding exponents, inverse operations, and the fundamental principle of balancing equations.
From simple algebraic manipulations to the profound nature of irrational numbers, this seemingly basic problem opens doors to a deeper appreciation for mathematics. It reminds us that every query, every equation, is an invitation to explore, learn, and discover the hidden patterns that govern our world.
Summary
The equation "x*x*x is equal to 2" is equivalent to `x^3 = 2`. To solve for 'x', one must take the cube root of both sides, yielding `x = ∛2`. This solution, the cube root of 2, is an irrational number, meaning its decimal representation is non-terminating and non-repeating. The process of solving this equation highlights fundamental algebraic principles, the concept of inverse operations, and introduces the fascinating world of irrational numbers, underscoring the multifaceted nature of mathematics.
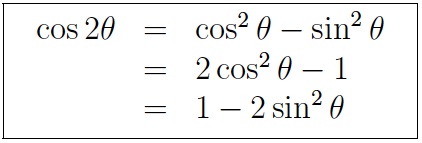
Summary of trigonometric identities

Lines and the Coordinate Plane: Graphing the Equation of a Line
Types of Vectors | GeeksforGeeks