Decoding The Equation: What Does X*x*x = X Really Mean?
The Foundation: Understanding x*x*x
Before we tackle the equation `x*x*x = x`, it's crucial to understand the expression `x*x*x` itself. In mathematics, when a variable or number is multiplied by itself multiple times, we use exponents to simplify the notation. The expression `x*x*x` is equal to `x^3`, which represents `x` raised to the power of 3. In mathematical notation, `x^3` means multiplying `x` by itself three times: `x × x × x`. This can also be referred to as "x cubed" or "x to the power of 3". It means a number being multiplied by itself for three times. For example, if `x=2`, then `x*x*x` becomes `2*2*2 = 8`. This concept is within the category of polynomials in mathematics. A polynomial is an expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. `X^3`, for instance, is a cubic polynomial, since out of the terms, it possesses the greatest power (which is 3). Understanding what `x*x*x` is equal to, or `x^3`, is a fundamental building block of algebra. It allows us to concisely represent repeated multiplication and forms the basis for more complex algebraic expressions and equations. The variable ‘x’ in algebra stands as a versatile symbol, representing an unknown value that we often aim to discover. This understanding of `x^3` is incredibly helpful in problem-solving, as it allows us to simplify expressions and set the stage for solving equations.Unraveling the Mystery: Solving x*x*x = x
Now that we grasp the meaning of `x*x*x`, let's turn our attention to the equation `x*x*x is equal to x`. Our goal is to solve for `x` — that is, find the number or numbers which, when multiplied by itself three times, equals `x` itself. This is a classic algebraic challenge that requires a systematic approach. Let’s break down this equation step by step to grasp its essence. First, we can rewrite the equation using exponential notation: `x^3 = x` To solve for `x`, we need to get all terms involving `x` on one side of the equation, setting the other side to zero. This is a common strategy when dealing with polynomials, as it allows us to use factoring techniques. 1. **Subtract `x` from both sides:** `x^3 - x = 0` This step is crucial. By subtracting `x` from both sides, we maintain the balance of the equation while preparing it for the next step: factorization. This aligns with general algebraic principles where we apply the same operation to both sides of an equation to isolate variables or simplify expressions. 2. **Factor out the common term:** Notice that both `x^3` and `x` share a common factor, which is `x`. We can factor `x` out of the expression: `x(x^2 - 1) = 0` This simplification leads us closer to finding the values of `x`. When we have a product of terms equal to zero, it means at least one of those terms must be zero. This is known as the Zero Product Property. 3. **Factor the difference of squares:** The term `(x^2 - 1)` is a special algebraic form known as a "difference of squares." It can be factored further into `(x - 1)(x + 1)`. So, our equation now becomes: `x(x - 1)(x + 1) = 0` This step is vital for revealing all possible solutions. It shows how simplifying the equation by grouping terms together and applying known algebraic identities can unlock solutions. 4. **Set each factor to zero and solve for `x`:** According to the Zero Product Property, for the entire expression to be zero, one or more of its factors must be zero. Therefore, we set each factor equal to zero and solve for `x`: * **Factor 1:** `x = 0` This is our first solution. * **Factor 2:** `x - 1 = 0` Add 1 to both sides: `x = 1` This is our second solution. * **Factor 3:** `x + 1 = 0` Subtract 1 from both sides: `x = -1` This is our third solution. So, the solutions for the equation `x*x*x = x` are `x = 0`, `x = 1`, and `x = -1`.Verifying the Solutions
It's always a good practice to verify your solutions by substituting them back into the original equation to confirm that they satisfy the equation. * **For x = 0:** `0 * 0 * 0 = 0` `0 = 0` (True) * **For x = 1:** `1 * 1 * 1 = 1` `1 = 1` (True) * **For x = -1:** `(-1) * (-1) * (-1) = -1` `1 * (-1) = -1` `-1 = -1` (True) All three solutions successfully satisfy the original equation. This systematic approach, breaking down the equation step by step, allows us to grasp its essence and arrive at the correct answers.Why This Matters: Beyond Just Numbers
Understanding and solving equations like `x*x*x = x` is more than just an academic exercise; it's about building foundational skills that are applicable across various fields. The variable ‘x’ in algebra stands as a versatile symbol, representing an unknown value that we seek to determine. This process helps us understand how things change and improve our ability to solve problems in math. Here’s why these fundamental building blocks of algebra are so important: * **Developing Problem-Solving Skills:** The systematic approach used to solve `x*x*x = x`—rewriting, simplifying, factoring, and verifying—is a template for tackling countless other mathematical and real-world problems. For those faced with the challenge of solving equations, a systematic approach is key. * **Grasping Algebraic Principles:** This exercise reinforces core algebraic principles such as the Zero Product Property, factoring techniques (like the difference of squares), and the importance of manipulating equations correctly by performing operations on both sides. Concepts like "subtract x from both sides" or "divide by 4 on both sides" are universal tools in algebra. * **Understanding Polynomials:** By working with `x^3`, we gain a practical understanding of cubic polynomials and how their properties (like having up to three real roots) influence their solutions. * **Foundation for Advanced Math:** Concepts learned from solving basic algebraic equations form the bedrock for more advanced topics, including calculus, where understanding how variables behave and change is paramount. Here, the seemingly elementary `x+x+x+x` is equal to `4x` transcends its origins, becoming a tool for understanding the fundamental principles that govern the calculus of change. * **Real-World Applications:** While `x*x*x = x` might seem abstract, the principles of solving for an unknown variable are used in fields from engineering and physics to economics and computer science. Whether it's calculating trajectories, optimizing processes, or predicting trends, the ability to solve for `x` is invaluable. In essence, every equation we solve, no matter how simple or complex, contributes to our overall mathematical literacy and logical reasoning abilities. Tools like online graphing calculators can further enhance this understanding by allowing us to visualize algebraic equations, plot points, and graph functions, adding another dimension to our learning.Summary
In summary, the expression `x*x*x` is simply `x^3`, or `x` multiplied by itself three times, falling into the category of cubic polynomials. When faced with the equation `x*x*x = x`, we can effectively solve it by transforming it into `x^3 - x = 0`. By factoring out `x` and then recognizing the difference of squares, we arrive at `x(x - 1)(x + 1) = 0`. This systematic algebraic approach reveals three distinct solutions for `x`: `0`, `1`, and `-1`. This exercise not only demonstrates fundamental algebraic principles like the Zero Product Property and factorization but also highlights the importance of methodical problem-solving in mathematics.
Find X if X is Rational Number Such That X X X Equal to X

x*x*x is Equal to | x*x*x equal to ? | Knowledge Glow
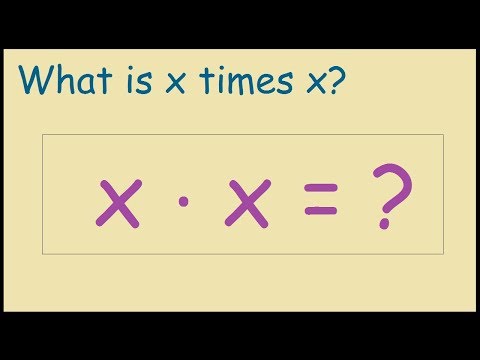
X Squared Plus X Squared Equals