Unlocking Algebraic Secrets: The Power And Meaning Of Factoring Expressions
Mathematics often presents us with intricate puzzles, expressions that look like a jumble of variables and numbers. Take, for instance, an expression like `x(x+1)(x-4)+4x+1`. At first glance, it might seem daunting. How do we make sense of it? How can we simplify it, or even use it to solve problems? This is where the crucial algebraic skill of "factoring" comes into play.
Factoring is one of the most fundamental operations in algebra, serving as a cornerstone for simplifying complex equations, solving for unknown variables, and understanding the behavior of functions. If you've ever wondered about the "meaning" behind transforming an expression, or how those online math solvers work their magic, understanding factoring is key. It's the reverse process of multiplication or "expanding" polynomials, allowing us to break down a larger expression into a product of simpler, more manageable components.
What Exactly is Factoring?
At its core, factoring is about rewriting an algebraic expression as a product of two or more factors. Think of it like breaking down a number into its prime factors. For example, the number 12 can be factored into 2 × 2 × 3. In algebra, we apply the same principle to expressions. The factoring calculator, for instance, "transforms complex expressions into a product of simpler factors." This means turning something like `x^2 - 7x + 12` into `(x - 3)(x - 4)`.
- Mountain Lion Kitten
- Artists Electronic Music Dj Gallium Ado
- Buc Ee S Ottine Photos
- 2009 Bmw Wagon Interior Tan
- Sofia Milos In Bikini
Why is this important? Because a factored expression reveals its underlying structure. It helps us find the "roots" of an equation (the values of x that make the expression equal to zero), simplify fractions involving polynomials, and even graph functions more easily. It's a critical step when you "solve an equation, inequality or a system."
Essential Factoring Techniques You Should Know
While the concept is straightforward, the techniques vary depending on the type of expression you're dealing with. Here are some of the most common methods:
1. Factoring Out the Greatest Common Factor (GCF)
This is often the first step in any factoring problem. It involves identifying the largest factor common to all terms in an expression and "taking it out."
Consider the example from our data: `3x^2(x + 2) + 2(x + 2)`.
Here, `(x + 2)` is the common factor in both terms. Following "Step 2: Take factor out of the common factor from each pair of expression," we can see it clearly. Then, "Step 3: Factor out the common binomial factor," which leads us to:
(x + 2)(3x^2 + 2)This technique is also applicable when the common factor is a single variable or number, like factoring `5x^2 + 10x` into `5x(x + 2)`.
2. Factoring Quadratic Expressions (ax² + bx + c)
Quadratic expressions are polynomials of degree two. Factoring them is a common task. For a simple quadratic like `x^2 + bx + c`, the goal is to find two numbers that "add up to b and multiply together to get c."
For example, to "factor quadratic x^2 - 7x + 12":
- We look for two numbers that multiply to 12 and add up to -7.
- These numbers are -3 and -4.
So, `x^2 - 7x + 12` factors into `(x - 3)(x - 4)`.
Similarly, for `x^2 + 5x + 4`, as mentioned in the data, "since 1 and 4 add up to 5 and multiply together to get 4, we can factor it like" `(x + 1)(x + 4)`.
3. Special Factoring Formulas
Certain patterns in expressions allow for quick factoring using specific formulas:
- Difference of Squares: `a^2 - b^2 = (a - b)(a + b)`
- Sum and Difference of Cubes: These are particularly useful for cubic expressions. As per the data, "For cubic expression we use the below mentioned formula for Sum of Cubes:"
a^3 + b^3 = (a + b)(a^2 - ab + b^2)4. Factoring by Grouping
This method is often used for polynomials with four or more terms. It involves grouping terms, factoring out a GCF from each group, and then factoring out a common binomial. The example `3x^2(x + 2) + 2(x + 2)` is a perfect illustration of the final step of factoring by grouping, where the common binomial `(x+2)` is factored out.
Navigating Complex Expressions and Real-World Problems
In actual math class, or when tackling more advanced problems, you rarely get "one skill at a time." As the data suggests, "These examples mix steps like distributing, factoring, reducing, and combining like terms." An expression like `x(x+1)(x-4)+4x+1)` might first require you to "expand polynomial" parts, then combine like terms, and only then attempt to factor the resulting polynomial. For instance, expanding `x(x+1)(x-4)` gives `x(x^2 - 3x - 4) = x^3 - 3x^2 - 4x`. Adding `4x+1` results in `x^3 - 3x^2 + 1`. Factoring such a cubic can be more challenging and might require advanced techniques or numerical methods, especially if it "has no rational root," meaning "there will no linear factor of f(x) and hence there will be no cubic factors also" over rational numbers.
This is where "online math solver with free step by step solutions to algebra, calculus, and other math problems" become invaluable. Tools like these allow you to "Enter the expression you want to factor in the editor" or "Type your algebra problem into the text box," providing "immediate feedback and guidance with step-by-step solutions." Whether it's finding the "GCD of x^4+2x^3-9x^2+46x-16 with x^4-8x^3+25x^2-46x+16" or the "quotient of x^3-8x^2+17x-6 with x-3," these resources can demystify complex operations.
Factoring and Solving Equations
One of the most powerful applications of factoring is solving equations. Once an equation is factored, we can use the Zero Product Property, which states that if a product of factors equals zero, then at least one of the factors must be zero. This allows us to find the "roots of x^2-3x+2" by factoring it into `(x-1)(x-2)=0`, leading to solutions `x=1` and `x=2`.
The "equation solver allows you to enter your problem and solve the equation to see the result," whether you "Solve in one variable or many." After finding a solution, it's always good practice to "Verifying the solution substitute your solution into the original equation to verify that it satisfies the equation."
Conclusion
Factoring is far more than just a mathematical exercise; it's a fundamental skill that empowers you to dissect, understand, and manipulate algebraic expressions. From simplifying basic quadratics to tackling more complex polynomials like `x(x+1)(x-4)+4x+1` (after expansion), the ability to factor transforms daunting equations into solvable puzzles. It's the key to finding roots, simplifying expressions, and building a strong foundation for advanced mathematics. With various techniques at your disposal and the aid of modern online solvers, mastering factoring becomes an achievable and incredibly rewarding endeavor in your mathematical journey.
- Chaos Paint
- Mitch Wilson Cause Of Death
- Vip Club Mineral Wells West Virginia
- Golfweek Amateur Tour
- Gabe Wilson

X X X X Factor X X 1 X 4 4 X 1 Meaning Means - Fill Online, Printable
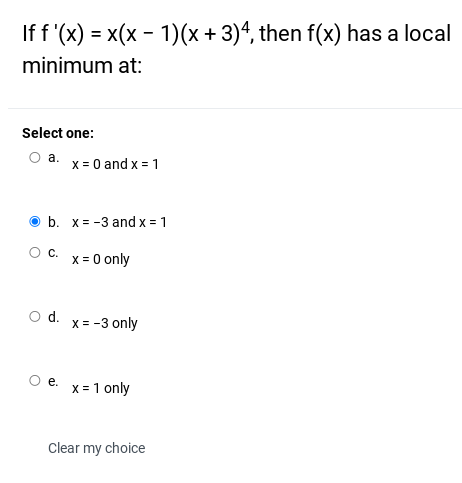
Solved If f'(x) = x(x - 1)(x + 3)4, then f(x) has a local | Chegg.com
^{4})
factor x^4-4x^3+6x^2-4x+1